 (vector densidad de corriente) es directamente proporcional a
(vector densidad de corriente) es directamente proporcional a  (vector campo eléctrico). Para escribir ésta relación en forma de ecuación es necesario añadir una constante arbitraria, que posteriormente se llamó factor de conductividad eléctrica y que representaremos como s. Entonces:
(vector campo eléctrico). Para escribir ésta relación en forma de ecuación es necesario añadir una constante arbitraria, que posteriormente se llamó factor de conductividad eléctrica y que representaremos como s. Entonces:El vector
 es el vector resultante de los campos que actúan en la sección de alambre que se va a analizar, es decir, del campo producido por la carga del alambre en sí y del campo externo, producido por una batería, una pila u otra fuente de fem. Por lo tanto:
es el vector resultante de los campos que actúan en la sección de alambre que se va a analizar, es decir, del campo producido por la carga del alambre en sí y del campo externo, producido por una batería, una pila u otra fuente de fem. Por lo tanto:Puesto que
 , donde
, donde 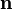 es un vector unitario tangente al filamento por el que circula la corriente, con lo cual reemplazamos y multiplicamos toda la ecuación por un
es un vector unitario tangente al filamento por el que circula la corriente, con lo cual reemplazamos y multiplicamos toda la ecuación por un 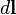 :
:Como los vectores
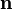 y
y 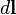 son paralelos su producto escalar coincide con el producto de sus magnitudes, además integrando ambos miembros en la longitud del conductor:
son paralelos su producto escalar coincide con el producto de sus magnitudes, además integrando ambos miembros en la longitud del conductor:El miembro derecho representa el trabajo total de los campos que actúan en la sección de alambre que se está analizando, y de cada integral resulta:
Donde φ1 − φ2 representa la diferencia de potencial entre los puntos 1 y 2, y ξ representa la fem; por tanto, podemos escribir:
donde U12 representa la caída de potencial entre los puntos 1 y 2.
Donde σ representa la conductividad, y su inversa representa la resistividad ρ = 1/σ. Así:
Finalmente, la expresión
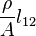 es lo que se conoce como resistencia eléctrica.
es lo que se conoce como resistencia eléctrica.Por tanto, podemos escribir la expresión final como lo dice abajo:

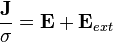





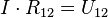
No hay comentarios:
Publicar un comentario