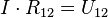Máxima transferencia de potencia
Se ha definido la potencia como la velocidad de producción de trabajo. Eléctricamente, la unidad de potencia es el vatio o watt "W". La relación de dependencia entre la potencia de c.c. "W" en una resistencia "R", la tensión "E" entre los extremos de "R", y la corriente "I" en "R" viene dada por la siguiente ecuación:
El teorema de máxima transferencia de potencia fue originalmente malinterpretado (notablemente por Joule) para sugerir que un sistema que consiste de un motor eléctrico comandado por una batería no podría superar el 50% de eficiencia pues, cuando las impedancias estuviesen adaptadas, la potencia perdida como caloren la batería sería siempre igual a la potencia entregada al motor.
En 1880, Edison (o su colega Francis Robbins Upton) muestraque esta suposición es falsa, al darse cuenta que la máxima eficiencia no es lo mismo que transferencia de máxima potencia. Para alcanzar la máxima eficiencia, la resistencia de la fuente (sea una batería o un dínamo) debería hacerse lo más pequeña posible.
Bajo la luz de este nuevo concepto, obtuvieron una eficiencia cercana al 90% y probaron que el motor eléctrico era una alternativa práctica al motor térmico.
En el circuito resulta que la máxima transferencia de potencia tiene lugar cuando la resistencia de la carga es igual a la resistencia interna del generador.
OBJETIVOS
• Determinar experimentalmente la condición necesaria para hallar la Máxima Transferencia de Potencia de un circuito eléctrico.
• Conocer los fundamentos básicos de este teorema.
• Analizar el comportamientode un circuito DC mediante la aplicación del principio de la Máxima Transferencia de Potencia.
FUNDAMENTO TEÓRICO
• 1. Enunciar la Ley que rige la Máxima Transferencia de Potencia.
Podemos enunciar la ley que rige la Máxima Transferencia de Potencia a una carga en un circuito de c.c.:
"Un generador transfiere la máxima potencia a una carga cuando la resistencia de ésta es igual a la resistencia interna del generador."
Puesto que cualquier red de c.c., terminada en una resistencia de carga RL puede ser transformada en un circuito equivalente constituido por un generador Thévenin VTH, con una resistencia interna RTH que alimenta la resistencia de carga RL.
La ley de máxima transferencia de potencia se puede generalizar como sigue:
"Cuando un red de c.c. está terminada por una resistencia de carga igual a sus resistencia de Thévenin, se desarrolla la máxima potencia en la resistencia de carga."
• 2. Definir el rendimiento de la Transferencia de Potencia.
El rendimiento nos proporciona la relación entre la potencia de entrada y la potencia de salida, es decir, entre el trabajoaplicado y el trabajo obtenido. Por ejemplo, en el caso de un transformador de corriente alterna, es la relación entre la potencia de salida aplicada a la carga y la potencia de entrada aplicada al transformador.
Ahora, determinaremos las condiciones en que obtendremos el máximo rendimiento de nuestra fuente de alimentación real, siendo el rendimiento igual a la relación entre la potencia entregada a la resistencia de carga y la potencia entregada por la fuente de tensión ideal
Donde podemos apreciar que obtenemos el rendimiento máximo para
Por lo que si deseamos obtener el máximo rendimiento del dispositivo que estamos diseñando, ya sea una fuente de alimentación, un generador o un transformador, tendremos que procurar que, la resistencia interna sea mucho menor que la resistencia de carga O bien, que la resistencia de carga sea mucho mayor que la resistencia interna
• 3. Describir el procedimiento para determinar la resistencia interna de una fuente de voltaje.
Para determinar la resistencia interna de cualquier fuente de alimentación real, podemos hacerlo mediante la medida de la tensión en circuito abierto y la corriente de cortocircuito de forma que :

 (vector
(vector  (vector
(vector 
 es el vector resultante de los campos que actúan en la sección de alambre que se va a analizar, es decir, del campo producido por la carga del alambre en sí y del campo externo, producido por una
es el vector resultante de los campos que actúan en la sección de alambre que se va a analizar, es decir, del campo producido por la carga del alambre en sí y del campo externo, producido por una 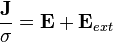
 , donde
, donde 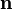 es un
es un 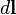 :
:




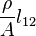 es lo que se conoce como
es lo que se conoce como